Remuestreo de Lanczos

Gráfico parcial de una señal discreta (puntos negros) y de su interpolación de Lanczos (curva azul continua), con el parámetro de tamaño a igual a 1 (arriba), 2 (en medio) y 3 (abajo). También se muestran dos copias del núcleo de Lanczos, desplazadas y escaladas, correspondientes a las muestras 4 y 11 (curvas de trazos).

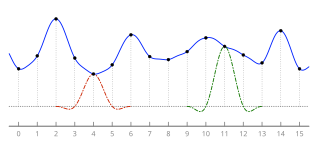
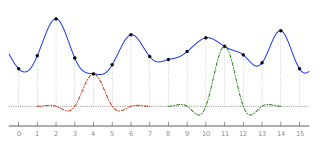
El remuestreo de Lanczos y el filtrado de Lanczos son dos aplicaciones de una fórmula matemática, que pueden usarse como filtro de paso bajo o para interpolar sin problemas el valor de una señal digital a partir de sus muestreos. En el último caso, asigna cada muestra de la señal dada a una copia trasladada y escalada del núcleo de Lanczos, que es una función ventana sinc por el lóbulo central de una segunda función sinc más larga. La suma de estos núcleos trasladados y escalados se evalúa luego en los puntos deseados.

El remuestreo de Lanczos se utiliza normalmente para aumentar el muestreo de una señal digital o para desplazarlo en una fracción del intervalo de muestreo. A menudo se usa también para la interpolación multivariable, como por ejemplo, para cambiar el tamaño o rotar una imagen digital. Se ha considerado el "mejor compromiso" entre varios filtros sencillos con estos propósitos.^[1]​

El filtro fue inventado por Claude Duchon, quien lo nombró así en referencia a Cornelius Lanczos debido al uso de la aproximación sigma en la construcción del filtro, una técnica creada por Lanczos.^[2]​

1. ↑ Turkowski, Ken; Gabriel, Steve (1990). «Filters for Common Resampling Tasks». En Glassner, Andrew S., ed. Graphics Gems I. Academic Press. pp. 147-165. ISBN 978-0-12-286165-9.  Parámetro desconocido |cite= ignorado (ayuda)
2. ↑ Claude, Duchon (1 de agosto de 1979). «Lanczos Filtering in One and Two Dimensions». Journal of Applied Meteorology 18 (8): 1016-1022. doi:10.1175/1520-0450(1979)018<1016:LFIOAT>2.0.CO;2.