Fonction affine

Cet article ne cite pas suffisamment ses sources (juillet 2023).

Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».

En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?

Fonction affine

Courbes représentatives des fonctions ${\displaystyle x\mapsto 0,5x+2}$ et ${\displaystyle x\mapsto -x+5}$.

Notation	${\displaystyle ax+b}$
Réciproque	${\displaystyle {\frac {1}{a}}x-{\frac {b}{a}}}$ si ${\displaystyle a\neq 0}$
Dérivée	${\displaystyle a}$
Primitives	${\displaystyle {\frac {a}{2}}x^{2}+bx+C}$

Principales caractéristiques

Ensemble de définition	${\displaystyle \mathbb {R} }$
Ensemble image	${\displaystyle \mathbb {R} }$ si ${\displaystyle a\neq 0}$

Valeurs particulières

Valeur en zéro	${\displaystyle b}$
Limite en +∞	${\displaystyle +\infty }$ si ${\displaystyle a>0}$ ${\displaystyle -\infty }$ si ${\displaystyle a<0}$
Limite en −∞	${\displaystyle -\infty }$ si ${\displaystyle a>0}$ ${\displaystyle +\infty }$ si ${\displaystyle a<0}$

Particularités

Zéros	${\displaystyle -{\frac {b}{a}}}$
Points fixes	${\displaystyle {\frac {b}{1-a}}}$ si ${\displaystyle a\neq 1}$

modifier - modifier le code - modifier Wikidata

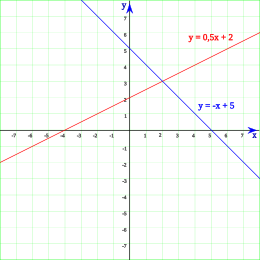
En analyse, une fonction affine est une fonction obtenue par addition et multiplication de la variable par des constantes. Elle peut donc s'écrire sous la forme :

${\displaystyle f(x)=ax+b}$

où les paramètres ${\displaystyle a}$ et ${\displaystyle b}$ ne dépendent pas de ${\displaystyle x}$^[1].

Lorsque la fonction est définie sur l'ensemble des réels, elle est représentée par une droite, dont ${\displaystyle a}$ est la pente et ${\displaystyle b}$ l'ordonnée à l'origine.

Un cas particulier des fonctions affines est lorsque l'ordonnée à l'origine est nulle, on obtient alors une fonction linéaire.

Les fonctions constantes et linéaires sont des exemples de fonctions affines. Les fonctions affines sont elles-mêmes des exemples de fonctions polynomiales de degré inférieur ou égal à 1.

La notion de fonction affine est généralisée en géométrie par celle d'application affine.

Remarque : dans certaines branches des mathématiques comme la statistique^[2], une telle fonction est appelée, à l'image du terme anglophone linear function et du terme allemand Lineare Funktion, une fonction linéaire en référence au fait que son graphe est une ligne droite.