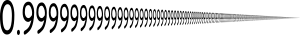
In mathematics, 0.999... (also written as 0.9, 0., or 0.(9)) denotes the smallest number greater than every number in the sequence (0.9, 0.99, 0.999, ...). It can be proved that this number is 1; that is,
Despite common misconceptions, 0.999... is not "almost exactly 1" or "very, very nearly but not quite 1"; rather, 0.999... and "1" are exactly the same number.
An elementary proof is given below that involves only elementary arithmetic and the fact that there is no positive real number less than all 1/10n, where n is a natural number, a property that results immediately from the Archimedean property of the real numbers.
There are many other ways of showing this equality, from intuitive arguments to mathematically rigorous proofs. The intuitive arguments are generally based on properties of finite decimals that are extended without proof to infinite decimals. The proofs are generally based on basic properties of real numbers and methods of calculus, such as series and limits. A question studied in mathematics education is why some people reject this equality.
In other number systems, 0.999... can have the same meaning, a different definition, or be undefined. Every nonzero terminating decimal has two equal representations (for example, 8.32000... and 8.31999...). Having values with multiple representations is a feature of all positional numeral systems that represent the real numbers.
