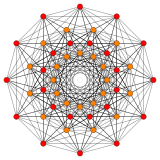
 122 |
 Rectified 122 |
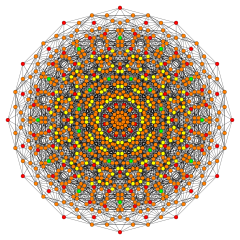 Birectified 122 |
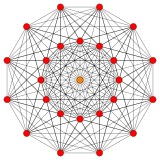 221 |
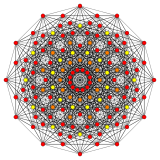 Rectified 221 | |
| orthogonal projections in E6 Coxeter plane | ||
|---|---|---|
In 6-dimensional geometry, the 122 polytope is a uniform polytope, constructed from the E6 group. It was first published in E. L. Elte's 1912 listing of semiregular polytopes, named as V72 (for its 72 vertices).[1]
Its Coxeter symbol is 122, describing its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 1-node sequence. There are two rectifications of the 122, constructed by positions points on the elements of 122. The rectified 122 is constructed by points at the mid-edges of the 122. The birectified 122 is constructed by points at the triangle face centers of the 122.
These polytopes are from a family of 39 convex uniform polytopes in 6-dimensions, made of uniform polytope facets and vertex figures, defined by all permutations of rings in this Coxeter-Dynkin diagram: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
- ^ Elte, 1912