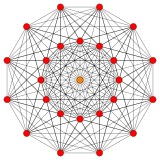
 221 |
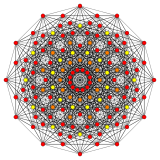 Rectified 221 | |
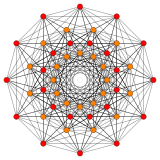 (122) |
 Birectified 221 (Rectified 122) | |
| orthogonal projections in E6 Coxeter plane | ||
|---|---|---|
In 6-dimensional geometry, the 221 polytope is a uniform 6-polytope, constructed within the symmetry of the E6 group. It was discovered by Thorold Gosset, published in his 1900 paper. He called it an 6-ic semi-regular figure.[1] It is also called the Schläfli polytope.
Its Coxeter symbol is 221, describing its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of one of the 2-node sequences. He also studied[2] its connection with the 27 lines on the cubic surface, which are naturally in correspondence with the vertices of 221.
The rectified 221 is constructed by points at the mid-edges of the 221. The birectified 221 is constructed by points at the triangle face centers of the 221, and is the same as the rectified 122.
These polytopes are a part of family of 39 convex uniform polytopes in 6-dimensions, made of uniform 5-polytope facets and vertex figures, defined by all permutations of rings in this Coxeter-Dynkin diagram: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
- ^ Gosset, 1900
- ^ Coxeter, H.S.M. (1940). "The Polytope 221 Whose Twenty-Seven Vertices Correspond to the Lines on the General Cubic Surface". Amer. J. Math. 62 (1): 457–486. doi:10.2307/2371466. JSTOR 2371466.