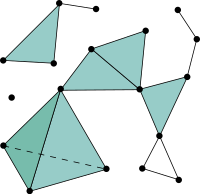
In combinatorics, an abstract simplicial complex (ASC), often called an abstract complex or just a complex, is a family of sets that is closed under taking subsets, i.e., every subset of a set in the family is also in the family. It is a purely combinatorial description of the geometric notion of a simplicial complex.[1] For example, in a 2-dimensional simplicial complex, the sets in the family are the triangles (sets of size 3), their edges (sets of size 2), and their vertices (sets of size 1).
In the context of matroids and greedoids, abstract simplicial complexes are also called independence systems.[2]
An abstract simplex can be studied algebraically by forming its Stanley–Reisner ring; this sets up a powerful relation between combinatorics and commutative algebra.
- ^ Lee, John M., Introduction to Topological Manifolds, Springer 2011, ISBN 1-4419-7939-5, p153
- ^ Korte, Bernhard; Lovász, László; Schrader, Rainer (1991). Greedoids. Springer-Verlag. p. 9. ISBN 3-540-18190-3.