Amicable numbers are two different natural numbers related in such a way that the sum of the proper divisors of each is equal to the other number. That is, s(a)=b and s(b)=a, where s(n)=σ(n)-n is equal to the sum of positive divisors of n except n itself (see also divisor function).
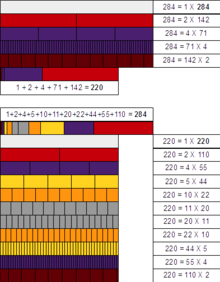
The smallest pair of amicable numbers is (220, 284). They are amicable because the proper divisors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110, of which the sum is 284; and the proper divisors of 284 are 1, 2, 4, 71 and 142, of which the sum is 220.
The first ten amicable pairs are: (220, 284), (1184, 1210), (2620, 2924), (5020, 5564), (6232, 6368), (10744, 10856), (12285, 14595), (17296, 18416), (63020, 76084), and (66928, 66992). (sequence A259180 in the OEIS). (Also see OEIS: A002025 and OEIS: A002046) It is unknown if there are infinitely many pairs of amicable numbers.
A pair of amicable numbers constitutes an aliquot sequence of period 2. A related concept is that of a perfect number, which is a number that equals the sum of its own proper divisors, in other words a number which forms an aliquot sequence of period 1. Numbers that are members of an aliquot sequence with period greater than 2 are known as sociable numbers.