
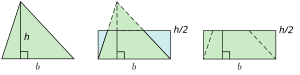
In geometry, calculating the area of a triangle is an elementary problem encountered often in many different situations. The best known and simplest formula is where b is the length of the base of the triangle, and h is the height or altitude of the triangle. The term "base" denotes any side, and "height" denotes the length of a perpendicular from the vertex opposite the base onto the line containing the base. Euclid proved that the area of a triangle is half that of a parallelogram with the same base and height in his book Elements in 300 BCE.[1] In 499 CE Aryabhata, used this illustrated method in the Aryabhatiya (section 2.6).[2]
Although simple, this formula is only useful if the height can be readily found, which is not always the case. For example, the land surveyor of a triangular field might find it relatively easy to measure the length of each side, but relatively difficult to construct a 'height'. Various methods may be used in practice, depending on what is known about the triangle. Other frequently used formulas for the area of a triangle use trigonometry, side lengths (Heron's formula), vectors, coordinates, line integrals, Pick's theorem, or other properties.[3]
- ^ "Euclid's Proof of the Pythagorean Theorem | Synaptic". Central College. Retrieved 2023-07-12.
- ^ The Āryabhaṭīya by Āryabhaṭa (translated into English by Walter Eugene Clark, 1930) hosted online by the Internet Archive.
- ^ Weisstein, Eric W. "Triangle area". MathWorld.

