Probability distribution
Beta|
Probability density function  |
|
Cumulative distribution function  |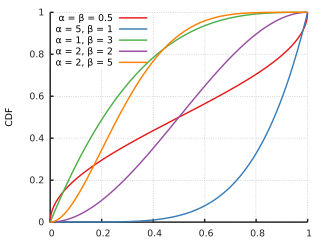
| Notation |
Beta(α, β) |
|---|
| Parameters |
α > 0 shape (real)
β > 0 shape (real) |
|---|
| Support |
 |
|---|
| PDF |
where  and  is the Gamma function. |
|---|
| CDF |
(the regularized incomplete beta function) |
|---|
| Mean |
![{\displaystyle \operatorname {E} [X]={\frac {\alpha }{\alpha +\beta }}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3905662ceed484cba5580951e29eda96f4d2605e)
![{\displaystyle \operatorname {E} [\ln X]=\psi (\alpha )-\psi (\alpha +\beta )\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de67df996fa33237ab7f415e7edc9fa8e71997a0)
![{\displaystyle \operatorname {E} [X\,\ln X]={\frac {\alpha }{\alpha +\beta }}\,\left[\psi (\alpha +1)-\psi (\alpha +\beta +1)\right]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50106a787db7d72ce3066a5a3238813cffebcc2e)
(see section: Geometric mean)
where  is the digamma function |
|---|
| Median |
![{\displaystyle {\begin{matrix}I_{\frac {1}{2}}^{[-1]}(\alpha ,\beta ){\text{ (in general) }}\\[0.5em]\approx {\frac {\alpha -{\tfrac {1}{3}}}{\alpha +\beta -{\tfrac {2}{3}}}}{\text{ for }}\alpha ,\beta >1\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af887ef0331cde970dad14ad670cf3592334f845) |
|---|
| Mode |
 for α, β > 1
Any value in the domain for α=β = 1
No mode if α<1 or β<1. Density diverges
at 0 for α ≤ 1, and at 1 if β ≤ 1 |
|---|
| Variance |
![{\displaystyle \operatorname {var} [X]={\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f90a6ad61b4b436749ca37a6c2a1aa077b032ce3)
![{\displaystyle \operatorname {var} [\ln X]=\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta )\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4941f45412823abd34d3befea7f8fbf544135e4)
(see trigamma function and see section: Geometric variance) |
|---|
| Skewness |
 |
|---|
| Excess kurtosis |
![{\displaystyle {\frac {6[(\alpha -\beta )^{2}(\alpha +\beta +1)-\alpha \beta (\alpha +\beta +2)]}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eea65a8d7c9e00ba6299b727eab679117776f41e) |
|---|
| Entropy |
![{\displaystyle {\begin{matrix}\ln \mathrm {B} (\alpha ,\beta )-(\alpha -1)\psi (\alpha )-(\beta -1)\psi (\beta )\\[0.5em]{}+(\alpha +\beta -2)\psi (\alpha +\beta )\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff4b6cc1848fe96318adb734393b701cb816f88a) |
|---|
| MGF |
 |
|---|
| CF |
 (see Confluent hypergeometric function) |
|---|
| Fisher information |
![{\displaystyle {\begin{bmatrix}\operatorname {var} [\ln X]&\operatorname {cov} [\ln X,\ln(1-X)]\\\operatorname {cov} [\ln X,\ln(1-X)]&\operatorname {var} [\ln(1-X)]\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/881f91af0ab1d6bf3809a4ed6ca9e6384544292f)
see section: Fisher information matrix |
|---|
| Method of moments |
}{V[X]}}-1\right)E[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2b596a180ef813a0baa1d6f2063950e20da1f62)
}{V[X]}}-1\right)(1-E[X])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05ace15e23f6ac9be43eea861f44c018fd3d00de) |
|---|
In probability theory and statistics, the beta distribution is a family of continuous probability distributions defined on the interval [0, 1] or (0, 1) in terms of two positive parameters, denoted by alpha (α) and beta (β), that appear as exponents of the variable and its complement to 1, respectively, and control the shape of the distribution.
The beta distribution has been applied to model the behavior of random variables limited to intervals of finite length in a wide variety of disciplines. The beta distribution is a suitable model for the random behavior of percentages and proportions.
In Bayesian inference, the beta distribution is the conjugate prior probability distribution for the Bernoulli, binomial, negative binomial, and geometric distributions.
The formulation of the beta distribution discussed here is also known as the beta distribution of the first kind, whereas beta distribution of the second kind is an alternative name for the beta prime distribution. The generalization to multiple variables is called a Dirichlet distribution.
