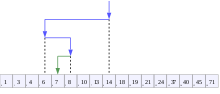
 Visualization of the binary search algorithm where 7 is the target value | |
| Class | Search algorithm |
|---|---|
| Data structure | Array |
| Worst-case performance | O(log n) |
| Best-case performance | O(1) |
| Average performance | O(log n) |
| Worst-case space complexity | O(1) |
| Optimal | Yes |
In computer science, binary search, also known as half-interval search,[1] logarithmic search,[2] or binary chop,[3] is a search algorithm that finds the position of a target value within a sorted array.[4][5] Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array.
Binary search runs in logarithmic time in the worst case, making comparisons, where is the number of elements in the array.[a][6] Binary search is faster than linear search except for small arrays. However, the array must be sorted first to be able to apply binary search. There are specialized data structures designed for fast searching, such as hash tables, that can be searched more efficiently than binary search. However, binary search can be used to solve a wider range of problems, such as finding the next-smallest or next-largest element in the array relative to the target even if it is absent from the array.
There are numerous variations of binary search. In particular, fractional cascading speeds up binary searches for the same value in multiple arrays. Fractional cascading efficiently solves a number of search problems in computational geometry and in numerous other fields. Exponential search extends binary search to unbounded lists. The binary search tree and B-tree data structures are based on binary search.
- ^ Williams, Jr., Louis F. (22 April 1976). A modification to the half-interval search (binary search) method. Proceedings of the 14th ACM Southeast Conference. ACM. pp. 95–101. doi:10.1145/503561.503582. Archived from the original on 12 March 2017. Retrieved 29 June 2018.
- ^ Knuth 1998, §6.2.1 ("Searching an ordered table"), subsection "Binary search".
- ^ Butterfield & Ngondi 2016, p. 46.
- ^ Cormen et al. 2009, p. 39.
- ^ Weisstein, Eric W. "Binary search". MathWorld.
- ^ Flores, Ivan; Madpis, George (1 September 1971). "Average binary search length for dense ordered lists". Communications of the ACM. 14 (9): 602–603. doi:10.1145/362663.362752. ISSN 0001-0782. S2CID 43325465.
Cite error: There are <ref group=lower-alpha> tags or {{efn}} templates on this page, but the references will not show without a {{reflist|group=lower-alpha}} template or {{notelist}} template (see the help page).

