This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|

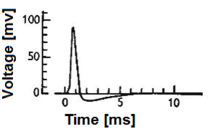
Biological neuron models, also known as spiking neuron models,[1] are mathematical descriptions of the conduction of electrical signals in neurons. Neurons (or nerve cells) are electrically excitable cells within the nervous system, able to fire electric signals, called action potentials, across a neural network. These mathematical models describe the role of the biophysical and geometrical characteristics of neurons on the conduction of electrical activity.
Central to these models is the description of how the membrane potential (that is, the difference in electric potential between the interior and the exterior of a biological cell) across the cell membrane changes over time. In an experimental setting, stimulating neurons with an electrical current generates an action potential (or spike), that propagates down the neuron's axon. This axon can branch out and connect to a large number of downstream neurons at sites called synapses. At these synapses, the spike can cause the release of neurotransmitters, which in turn can change the voltage potential of downstream neurons. This change can potentially lead to even more spikes in those downstream neurons, thus passing down the signal. As many as 95% of neurons in the neocortex, the outermost layer of the mammalian brain, consist of excitatory pyramidal neurons,[2][3] and each pyramidal neuron receives tens of thousands of inputs from other neurons.[4] Thus, spiking neurons are a major information processing unit of the nervous system.
One such example of a spiking neuron model may be a highly detailed mathematical model that includes spatial morphology. Another may be a conductance-based neuron model that views neurons as points and describes the membrane voltage dynamics as a function of trans-membrane currents. A mathematically simpler "integrate-and-fire" model significantly simplifies the description of ion channel and membrane potential dynamics (initially studied by Lapique in 1907).[5][6]
- ^ Gerstner W, Kistler WM (2002). Spiking neuron models : single neurons, populations, plasticity. Cambridge, U.K.: Cambridge University Press. ISBN 0-511-07817-X. OCLC 57417395.
- ^ DeFelipe, Javier; Farinas, Isabel (1992). "The pyramidal neuron of the cerebral cortex: morphological and chemical characteristics of the synaptic inputs". Progress in Neurobiology. 39 (6): 563–607. doi:10.1016/0301-0082(92)90015-7. PMID 1410442. S2CID 34889543.
- ^ Markram, Henry; Muller, Eilif; Ramaswamy, Srikanth; Reimann, Michael; Abdellah, Marwan (2015). "Reconstruction and simulation of neocortical microcircuitry". Cell. 163 (2): 456–492. doi:10.1016/j.cell.2015.09.029. PMID 26451489. S2CID 14466831.
- ^ Wong, R. K. S.; Traub, R. D. (2009-01-01), "NETWORKS | Cellular Properties and Synaptic Connectivity of CA3 Pyramidal Cells: Mechanisms for Epileptic Synchronization and Epileptogenesis", in Schwartzkroin, Philip A. (ed.), Encyclopedia of Basic Epilepsy Research, Oxford: Academic Press, pp. 815–819, doi:10.1016/b978-012373961-2.00215-0, ISBN 978-0-12-373961-2, retrieved 2020-11-18
- ^ Lapicque, LM (1907). "Recherches quantitatives sur l'excitation electrique des nerfs". J Physiol Paris. 9: 620–635.
- ^ Abbott, Larry (1999). "Lapicque's introduction of the integrate-and-fire model neuron (1907)". Brain Research Bulletin. 50 (5): 303–304. doi:10.1016/S0361-9230(99)00161-6. PMID 10643408. S2CID 46170924.