In relativistic physics, the Born coordinate chart is a coordinate chart for (part of) Minkowski spacetime, the flat spacetime of special relativity. It is often used to analyze the physical experience of observers who ride on a ring or disk rigidly rotating at relativistic speeds, so called Langevin observers. This chart is often attributed to Max Born, due to his 1909 work on the relativistic physics of a rotating body. For overview of the application of accelerations in flat spacetime, see Acceleration (special relativity) and proper reference frame (flat spacetime).
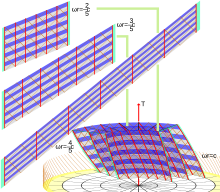
From experience by inertial scenarios (i.e. measurements in inertial frames), Langevin observers synchronize their clocks by standard Einstein convention or by slow clock synchronization, respectively (both internal synchronizations). For a certain Langevin observer this method works perfectly. Within its immediate vicinity clocks are synchronized and light propagates isotropically in space. But the experience when the observers try to synchronize their clocks along a closed path in space is puzzling: there are always at least two neighboring clocks which have different times. To remedy the situation, the observers agree on an external synchronization procedure (coordinate time t — or for ring-riding observers, a proper coordinate time for a fixed radius r). By this agreement, Langevin observers riding on a rigidly rotating disk will conclude from measurements of small distances between themselves that the geometry of the disk is non-Euclidean. Regardless of which method they use, they will conclude that the geometry is well approximated by a certain Riemannian metric, namely the Langevin–Landau–Lifschitz metric. This is in turn very well approximated by the geometry of the hyperbolic plane (with the negative curvatures −3ω2 and −3ω2 r2 respectively). But if these observers measure larger distances, they will obtain different results, depending upon which method of measurement they use! In all such cases, however, they will most likely obtain results which are inconsistent with any Riemannian metric. In particular, if they use the simplest notion of distance, radar distance, owing to various effects such as the asymmetry already noted, they will conclude that the "geometry" of the disk is not only non-Euclidean, it is non-Riemannian.
The rotating disk is not a paradox. Whatever method the observers use to analyze the situation: at the end they find themselves analyzing a rotating disk and not an inertial frame.