This article needs additional citations for verification. (September 2021) |
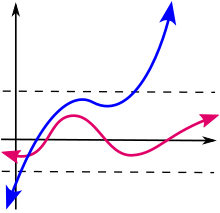
In mathematics, a function defined on some set with real or complex values is called bounded if the set of its values is bounded. In other words, there exists a real number such that
for all in .[1] A function that is not bounded is said to be unbounded.[citation needed]
If is real-valued and for all in , then the function is said to be bounded (from) above by . If for all in , then the function is said to be bounded (from) below by . A real-valued function is bounded if and only if it is bounded from above and below.[1][additional citation(s) needed]
An important special case is a bounded sequence, where is taken to be the set of natural numbers. Thus a sequence is bounded if there exists a real number such that
for every natural number . The set of all bounded sequences forms the sequence space .[citation needed]
The definition of boundedness can be generalized to functions taking values in a more general space by requiring that the image is a bounded set in .[citation needed]
- ^ a b Jeffrey, Alan (1996-06-13). Mathematics for Engineers and Scientists, 5th Edition. CRC Press. ISBN 978-0-412-62150-5.
















