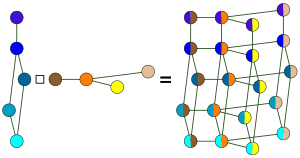
In graph theory, the Cartesian product G □ H of graphs G and H is a graph such that:
- the vertex set of G □ H is the Cartesian product V(G) × V(H); and
- two vertices (u,v) and (u' ,v' ) are adjacent in G □ H if and only if either
- u = u' and v is adjacent to v' in H, or
- v = v' and u is adjacent to u' in G.
The Cartesian product of graphs is sometimes called the box product of graphs [Harary 1969].
The operation is associative, as the graphs (F □ G) □ H and F □ (G □ H) are naturally isomorphic. The operation is commutative as an operation on isomorphism classes of graphs, and more strongly the graphs G □ H and H □ G are naturally isomorphic, but it is not commutative as an operation on labeled graphs.
The notation G × H has often been used for Cartesian products of graphs, but is now more commonly used for another construction known as the tensor product of graphs. The square symbol is intended to be an intuitive and unambiguous notation for the Cartesian product, since it shows visually the four edges resulting from the Cartesian product of two edges.[1]