Category of relations

Rel
Category of Relations Rel.
Relop
Rel's opposite Relop.

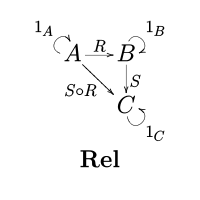
In mathematics, the category Rel has the class of sets as objects and binary relations as morphisms.

A morphism (or arrow) R : A → B in this category is a relation between the sets A and B, so R ⊆ A × B.

The composition of two relations R: A → B and S: B → C is given by

(a, c) ∈ S o R ⇔ for some b ∈ B, (a, b) ∈ R and (b, c) ∈ S.[1]

Rel has also been called the "category of correspondences of sets".[2]

  1. ^ Mac Lane, S. (1988). Categories for the Working Mathematician (1st ed.). Springer. p. 26. ISBN 0-387-90035-7.
  2. ^ Pareigis, Bodo (1970). Categories and Functors. Pure and Applied Mathematics. Vol. 39. Academic Press. p. 6. ISBN 978-0-12-545150-5.