
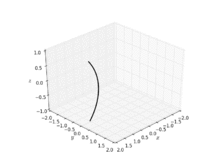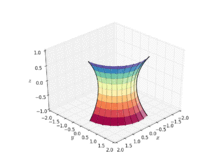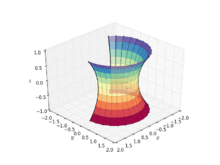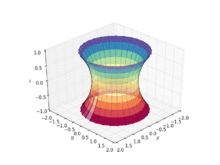
In geometry, a catenoid is a type of surface, arising by rotating a catenary curve about an axis (a surface of revolution).[1] It is a minimal surface, meaning that it occupies the least area when bounded by a closed space.[2] It was formally described in 1744 by the mathematician Leonhard Euler.
Soap film attached to twin circular rings will take the shape of a catenoid.[2] Because they are members of the same associate family of surfaces, a catenoid can be bent into a portion of a helicoid, and vice versa.
- ^ Dierkes, Ulrich; Hildebrandt, Stefan; Sauvigny, Friedrich (2010). Minimal Surfaces. Springer Science & Business Media. p. 141. ISBN 9783642116988.
- ^ a b Gullberg, Jan (1997). Mathematics: From the Birth of Numbers. W. W. Norton & Company. p. 538. ISBN 9780393040029.