Chi-squared distribution

Chi-squared

Probability density function
Cumulative distribution function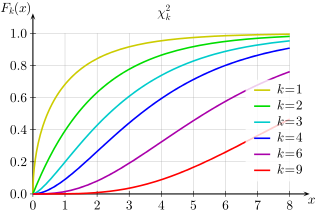
Notation	${\displaystyle \chi ^{2}(k)\;}$ or ${\displaystyle \chi _{k}^{2}\!}$
Parameters	${\displaystyle k\in \mathbb {N} ^{*}~~}$ (known as "degrees of freedom")
Support	${\displaystyle x\in (0,+\infty )\;}$
PDF	${\displaystyle {\frac {1}{2^{k/2}\Gamma (k/2)}}\;x^{k/2-1}e^{-x/2}\;}$
CDF	${\displaystyle {\frac {1}{\Gamma (k/2)}}\;\gamma \left({\frac {k}{2}},\,{\frac {x}{2}}\right)\;}$
Mean	${\displaystyle k}$
Median	${\displaystyle \approx k{\bigg (}1-{\frac {2}{9k}}{\bigg )}^{3}\;}$
Mode	${\displaystyle \max(k-2,0)\;}$
Variance	${\displaystyle 2k\;}$
Skewness	${\displaystyle {\sqrt {8/k}}\,}$
Excess kurtosis	${\displaystyle {\frac {12}{k}}}$
Entropy	${\displaystyle {\begin{aligned}{\frac {k}{2}}&+\log \left(2\Gamma {\Bigl (}{\frac {k}{2}}{\Bigr )}\right)\\&\!+\left(1-{\frac {k}{2}}\right)\psi \left({\frac {k}{2}}\right)\end{aligned}}}$
MGF	${\displaystyle (1-2t)^{-k/2}{\text{ for }}t<{\frac {1}{2}}\;}$
CF	${\displaystyle (1-2it)^{-k/2}}$[1]
PGF	${\displaystyle (1-2\ln t)^{-k/2}{\text{ for }}0<t<{\sqrt {e}}\;}$

In probability theory and statistics, the chi-squared distribution (also chi-square or ${\displaystyle \chi ^{2}}$-distribution) with ${\displaystyle k}$ degrees of freedom is the distribution of a sum of the squares of ${\displaystyle k}$ independent standard normal random variables.^[2]

The chi-squared distribution ${\displaystyle \chi _{k}^{2}}$ is a special case of the gamma distribution and the univariate Wishart distribution. Specifically if ${\displaystyle X\sim \chi _{k}^{2}}$ then ${\displaystyle X\sim {\text{Gamma}}(\alpha ={\frac {k}{2}},\theta =2)}$ (where ${\displaystyle \alpha }$ is the shape parameter and ${\displaystyle \theta }$ the scale parameter of the gamma distribution) and ${\displaystyle X\sim {\text{W}}_{1}(1,k)}$.

The scaled chi-squared distribution ${\displaystyle s^{2}\chi _{k}^{2}}$ is a reparametrization of the gamma distribution and the univariate Wishart distribution. Specifically if ${\displaystyle X\sim s^{2}\chi _{k}^{2}}$ then ${\displaystyle X\sim {\text{Gamma}}(\alpha ={\frac {k}{2}},\theta =2s^{2})}$ and ${\displaystyle X\sim {\text{W}}_{1}(s^{2},k)}$.

The chi-squared distribution is one of the most widely used probability distributions in inferential statistics, notably in hypothesis testing and in construction of confidence intervals.^[3][4][5][6] This distribution is sometimes called the central chi-squared distribution, a special case of the more general noncentral chi-squared distribution.^[7]

The chi-squared distribution is used in the common chi-squared tests for goodness of fit of an observed distribution to a theoretical one, the independence of two criteria of classification of qualitative data, and in finding the confidence interval for estimating the population standard deviation of a normal distribution from a sample standard deviation. Many other statistical tests also use this distribution, such as Friedman's analysis of variance by ranks.