In number theory, a congruent number is a positive integer that is the area of a right triangle with three rational number sides.[1][2] A more general definition includes all positive rational numbers with this property.[3]
The sequence of (integer) congruent numbers starts with
- 5, 6, 7, 13, 14, 15, 20, 21, 22, 23, 24, 28, 29, 30, 31, 34, 37, 38, 39, 41, 45, 46, 47, 52, 53, 54, 55, 56, 60, 61, 62, 63, 65, 69, 70, 71, 77, 78, 79, 80, 84, 85, 86, 87, 88, 92, 93, 94, 95, 96, 101, 102, 103, 109, 110, 111, 112, 116, 117, 118, 119, 120, ... (sequence A003273 in the OEIS)
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| — | — | — | — | C | C | C | — | |
| n | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| — | — | — | — | C | C | C | — | |
| n | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| — | — | — | S | C | C | C | S | |
| n | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
| — | — | — | S | C | C | C | — | |
| n | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| — | C | — | — | C | C | C | — | |
| n | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 |
| C | — | — | — | S | C | C | — | |
| n | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 |
| — | — | — | S | C | S | C | S | |
| n | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 |
| — | — | — | S | C | C | S | — | |
| n | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 |
| C | — | — | — | C | C | C | — | |
| n | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| — | — | — | — | C | C | C | S | |
| n | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 |
| — | — | — | S | C | C | C | S | |
| n | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 |
| — | — | — | S | C | C | C | S | |
| n | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 |
| — | — | — | — | C | C | C | — | |
| n | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 |
| — | — | — | — | C | C | C | S | |
| n | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 |
| — | — | — | S | S | C | C | S |
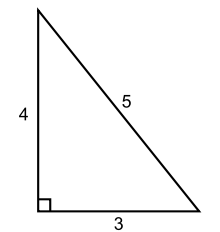
For example, 5 is a congruent number because it is the area of a (20/3, 3/2, 41/6) triangle. Similarly, 6 is a congruent number because it is the area of a (3,4,5) triangle. 3 and 4 are not congruent numbers.
If q is a congruent number then s2q is also a congruent number for any natural number s (just by multiplying each side of the triangle by s), and vice versa. This leads to the observation that whether a nonzero rational number q is a congruent number depends only on its residue in the group
where is the set of nonzero rational numbers.
Every residue class in this group contains exactly one square-free integer, and it is common, therefore, only to consider square-free positive integers, when speaking about congruent numbers.
- ^ Weisstein, Eric W. "Congruent Number". MathWorld.
- ^ Guy, Richard K. (2004). Unsolved problems in number theory ([3rd ed.] ed.). New York: Springer. pp. 195–197. ISBN 0-387-20860-7. OCLC 54611248.
- ^ Koblitz, Neal (1993), Introduction to Elliptic Curves and Modular Forms, New York: Springer-Verlag, p. 3, ISBN 0-387-97966-2

