Cross-polytope

Cross-polytopes of dimension 2 to 5
A 2-dimensional cross-polytope A 3-dimensional cross-polytope
2 dimensions
square 		3 dimensions
octahedron
A 4-dimensional cross-polytope A 5-dimensional cross-polytope
4 dimensions
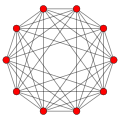
16-cell 		5 dimensions
5-orthoplex

In geometry, a cross-polytope,[1] hyperoctahedron, orthoplex,[2] staurotope,[3] or cocube is a regular, convex polytope that exists in n-dimensional Euclidean space. A 2-dimensional cross-polytope is a square, a 3-dimensional cross-polytope is a regular octahedron, and a 4-dimensional cross-polytope is a 16-cell. Its facets are simplexes of the previous dimension, while the cross-polytope's vertex figure is another cross-polytope from the previous dimension.

The vertices of a cross-polytope can be chosen as the unit vectors pointing along each co-ordinate axis – i.e. all the permutations of (±1, 0, 0, ..., 0). The cross-polytope is the convex hull of its vertices. The n-dimensional cross-polytope can also be defined as the closed unit ball (or, according to some authors, its boundary) in the ℓ1-norm on Rn:

In 1 dimension the cross-polytope is simply the line segment [−1, +1], in 2 dimensions it is a square (or diamond) with vertices {(±1, 0), (0, ±1)}. In 3 dimensions it is an octahedron—one of the five convex regular polyhedra known as the Platonic solids. This can be generalised to higher dimensions with an n-orthoplex being constructed as a bipyramid with an (n−1)-orthoplex base.

The cross-polytope is the dual polytope of the hypercube. The 1-skeleton of an n-dimensional cross-polytope is the Turán graph T(2n, n) (also known as a cocktail party graph [4]).

  1. ^ Coxeter 1973, pp. 121–122, §7.21. illustration Fig 7-2B.
  2. ^ Conway, J. H.; Sloane, N. J. A. (1991). "The Cell Structures of Certain Lattices". In Hilton, P.; Hirzebruch, F.; Remmert, R. (eds.). Miscellanea Mathematica. Berlin: Springer. pp. 89–90. doi:10.1007/978-3-642-76709-8_5. ISBN 978-3-642-76711-1.
  3. ^ McMullen, Peter (2020). Geometric Regular Polytopes. Cambridge University Press. p. 92. ISBN 978-1-108-48958-4.
  4. ^ Weisstein, Eric W. "Cocktail Party Graph". MathWorld.