Cross-polytope

Cross-polytopes of dimension 2 to 5

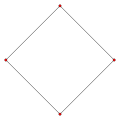
2 dimensions square	3 dimensions octahedron
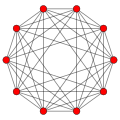
4 dimensions 16-cell	5 dimensions 5-orthoplex

In geometry, a cross-polytope,^[1] hyperoctahedron, orthoplex,^[2] or cocube is a regular, convex polytope that exists in n-dimensional Euclidean space. A 2-dimensional cross-polytope is a square, a 3-dimensional cross-polytope is a regular octahedron, and a 4-dimensional cross-polytope is a 16-cell. Its facets are simplexes of the previous dimension, while the cross-polytope's vertex figure is another cross-polytope from the previous dimension.

The vertices of a cross-polytope can be chosen as the unit vectors pointing along each co-ordinate axis – i.e. all the permutations of (±1, 0, 0, ..., 0). The cross-polytope is the convex hull of its vertices. The n-dimensional cross-polytope can also be defined as the closed unit ball (or, according to some authors, its boundary) in the ℓ₁-norm on Rⁿ:

${\displaystyle \{x\in \mathbb {R} ^{n}:\|x\|_{1}\leq 1\}.}$

In 1 dimension the cross-polytope is simply the line segment [−1, +1], in 2 dimensions it is a square (or diamond) with vertices {(±1, 0), (0, ±1)}. In 3 dimensions it is an octahedron—one of the five convex regular polyhedra known as the Platonic solids. This can be generalised to higher dimensions with an n-orthoplex being constructed as a bipyramid with an (n−1)-orthoplex base.

The cross-polytope is the dual polytope of the hypercube. The 1-skeleton of an n-dimensional cross-polytope is the Turán graph T(2n, n) (also known as a cocktail party graph ^[3]).