Cumulative distribution function

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Cumulative distribution function" – news · newspapers · books · scholar · JSTOR (March 2010) (Learn how and when to remove this message)

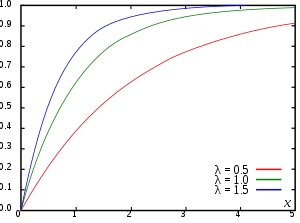
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable ${\displaystyle X}$, or just distribution function of ${\displaystyle X}$, evaluated at ${\displaystyle x}$, is the probability that ${\displaystyle X}$ will take a value less than or equal to ${\displaystyle x}$.^[1]

Every probability distribution supported on the real numbers, discrete or "mixed" as well as continuous, is uniquely identified by a right-continuous monotone increasing function (a càdlàg function) ${\displaystyle F\colon \mathbb {R} \rightarrow [0,1]}$ satisfying ${\displaystyle \lim _{x\rightarrow -\infty }F(x)=0}$ and ${\displaystyle \lim _{x\rightarrow \infty }F(x)=1}$.

In the case of a scalar continuous distribution, it gives the area under the probability density function from negative infinity to ${\displaystyle x}$. Cumulative distribution functions are also used to specify the distribution of multivariate random variables.