In mathematics, the curve-shortening flow is a process that modifies a smooth curve in the Euclidean plane by moving its points perpendicularly to the curve at a speed proportional to the curvature. The curve-shortening flow is an example of a geometric flow, and is the one-dimensional case of the mean curvature flow. Other names for the same process include the Euclidean shortening flow, geometric heat flow,[1] and arc length evolution.
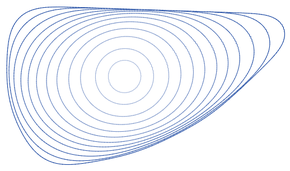
As the points of any smooth simple closed curve move in this way, the curve remains simple and smooth. It loses area at a constant rate, and its perimeter decreases as quickly as possible for any continuous curve evolution. If the curve is non-convex, its total absolute curvature decreases monotonically, until it becomes convex. Once convex, the isoperimetric ratio of the curve decreases as the curve converges to a circular shape, before collapsing to a singularity. If two disjoint simple smooth closed curves evolve, they remain disjoint until one of them collapses to a point. The circle is the only simple closed curve that maintains its shape under the curve-shortening flow, but some curves that cross themselves or have infinite length keep their shape, including the grim reaper curve, an infinite curve that translates upwards, and spirals that rotate while remaining the same size and shape.
An approximation to the curve-shortening flow can be computed numerically, by approximating the curve as a polygon and using the finite difference method to calculate the motion of each polygon vertex. Alternative methods include computing a convolution of polygon vertices and then resampling vertices on the resulting curve, or repeatedly applying a median filter to a digital image whose black and white pixels represent the inside and outside of the curve.
The curve-shortening flow was originally studied as a model for annealing of metal sheets. Later, it was applied in image analysis to give a multi-scale representation of shapes. It can also model reaction–diffusion systems, and the behavior of cellular automata. The curve-shortening flow can be used to find closed geodesics on Riemannian manifolds, and as a model for the behavior of higher-dimensional flows.
- ^ The phrase "geometric heat flow" has also been used for flows on other kinds of object than curves, such as differential forms.