| Desargues graph | |
|---|---|
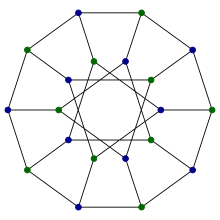 | |
| Named after | Gérard Desargues |
| Vertices | 20 |
| Edges | 30 |
| Radius | 5 |
| Diameter | 5 |
| Girth | 6 |
| Automorphisms | 240 (S5 × S2) |
| Chromatic number | 2 |
| Chromatic index | 3 |
| Genus | 2 |
| Book thickness | 3 |
| Queue number | 2 |
| Properties | Cubic Distance-regular Hamiltonian Bipartite Symmetric |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the Desargues graph is a distance-transitive, cubic graph with 20 vertices and 30 edges.[1] It is named after Girard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial cube, and has been applied in chemical databases.
The name "Desargues graph" has also been used to refer to a ten-vertex graph, the complement of the Petersen graph, which can also be formed as the bipartite half of the 20-vertex Desargues graph.[2]
- ^ Weisstein, Eric W., "Desargues Graph", MathWorld
- ^ Kagno, I. N. (1947), "Desargues' and Pappus' graphs and their groups", American Journal of Mathematics, 69 (4), The Johns Hopkins University Press: 859–863, doi:10.2307/2371806, JSTOR 2371806.