This article needs additional citations for verification. (August 2012) |
| Regular dodecagram | |
|---|---|
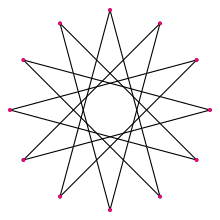 A regular dodecagram | |
| Type | Regular star polygon |
| Edges and vertices | 12 |
| Schläfli symbol | {12/5} t{6/5} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | Dihedral (D12) |
| Internal angle (degrees) | 30° |
| Properties | star, cyclic, equilateral, isogonal, isotoxal |
| Dual polygon | self |
| Star polygons |
|---|
|
|
In geometry, a dodecagram (from Greek δώδεκα (dṓdeka) 'twelve' and γραμμῆς (grammēs) 'line'[1]) is a star polygon or compound with 12 vertices. There is one regular dodecagram polygon (with Schläfli symbol {12/5} and a turning number of 5). There are also 4 regular compounds {12/2}, {12/3}, {12/4}, and {12/6}.