| Set of uniform p-q duoprisms | |
| Type | Prismatic uniform 4-polytopes |
| Schläfli symbol | {p}×{q} |
| Coxeter-Dynkin diagram | |
| Cells | p q-gonal prisms, q p-gonal prisms |
| Faces | pq squares, p q-gons, q p-gons |
| Edges | 2pq |
| Vertices | pq |
| Vertex figure | 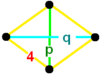 disphenoid |
| Symmetry | [p,2,q], order 4pq |
| Dual | p-q duopyramid |
| Properties | convex, vertex-uniform |
| Set of uniform p-p duoprisms | |
| Type | Prismatic uniform 4-polytope |
| Schläfli symbol | {p}×{p} |
| Coxeter-Dynkin diagram | |
| Cells | 2p p-gonal prisms |
| Faces | p2 squares, 2p p-gons |
| Edges | 2p2 |
| Vertices | p2 |
| Symmetry | [p,2,p] = [2p,2+,2p], order 8p2 |
| Dual | p-p duopyramid |
| Properties | convex, vertex-uniform, Facet-transitive |

In geometry of 4 dimensions or higher, a double prism[1] or duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an n-polytope and an m-polytope is an (n+m)-polytope, where n and m are dimensions of 2 (polygon) or higher.
The lowest-dimensional duoprisms exist in 4-dimensional space as 4-polytopes being the Cartesian product of two polygons in 2-dimensional Euclidean space. More precisely, it is the set of points:
where P1 and P2 are the sets of the points contained in the respective polygons. Such a duoprism is convex if both bases are convex, and is bounded by prismatic cells.
- ^ The Fourth Dimension Simply Explained, Henry P. Manning, Munn & Company, 1910, New York. Available from the University of Virginia library. Also accessible online: The Fourth Dimension Simply Explained—contains a description of duoprisms (double prisms) and duocylinders (double cylinders). Googlebook
