 A regular tiling has one type of regular face. |
 A semiregular or uniform tiling has one type of vertex, but two or more types of faces. |
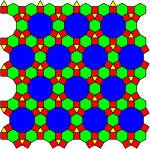 A k-uniform tiling has k types of vertices, and two or more types of regular faces. |
 A non-edge-to-edge tiling can have different-sized regular faces. |
Euclidean plane tilings by convex regular polygons have been widely used since antiquity. The first systematic mathematical treatment was that of Kepler in his Harmonices Mundi (Latin: The Harmony of the World, 1619).