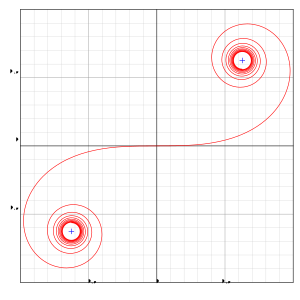
An Euler spiral is a curve whose curvature changes linearly with its curve length (the curvature of a circular curve is equal to the reciprocal of the radius). This curve is also referred to as a clothoid or Cornu spiral.[1][2] The behavior of Fresnel integrals can be illustrated by an Euler spiral, a connection first made by Marie Alfred Cornu in 1874.[3] Euler's spiral is a type of superspiral that has the property of a monotonic curvature function.[4]
The Euler spiral has applications to diffraction computations. They are also widely used in railway and highway engineering to design transition curves between straight and curved sections of railways or roads. A similar application is also found in photonic integrated circuits. The principle of linear variation of the curvature of the transition curve between a tangent and a circular curve defines the geometry of the Euler spiral:
- Its curvature begins with zero at the straight section (the tangent) and increases linearly with its curve length.
- Where the Euler spiral meets the circular curve, its curvature becomes equal to that of the latter.
- ^ Von Seggern, David H. (1994). Practical handbook of curve design and generation. Boca Raton, Fla.: CRC Press. ISBN 978-0-8493-8916-0.
- ^ Levien, Raph. "The Euler spiral: a mathematical history." Rapp. tech (2008).
- ^ Marie Alfred Cornu. M´ethode nouvelle pour la discussion des probl´emes de diffraction dans le cas d’une onde cylindrique. Journal de Physique th´eoretique et appliqu´ee, pages 5–15, 1874.
- ^ Ziatdinov, R. (2012), "Family of superspirals with completely monotonic curvature given in terms of Gauss hypergeometric function", Computer Aided Geometric Design, 29 (7): 510–518, doi:10.1016/j.cagd.2012.03.006