In mathematics, the extended real number system[a] is obtained from the real number system by adding two elements denoted and [b] that are respectively greater and lower than every real number. This allows for treating the potential infinities of infinitely increasing sequences and infinitely decreasing series as actual infinities. For example, the infinite sequence of the natural numbers increases infinitively and has no upper bound in the real number system (a potential infinity); in the extended real number line, the sequence has as its least upper bound and as its limit (an actual infinity). In calculus and mathematical analysis, the use of and as actual limits extends significantly the possible computations.[1] It is the Dedekind–MacNeille completion of the real numbers.
The extended real number system is denoted or or [2] When the meaning is clear from context, the symbol is often written simply as [2]
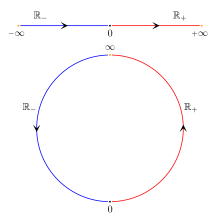
There is also a distinct projectively extended real line where and are not distinguished, i.e., there is a single actual infinity for both infinitely increasing sequences and infinitely decreasing sequences that is denoted as just or as .
Cite error: There are <ref group=lower-alpha> tags or {{efn}} templates on this page, but the references will not show without a {{reflist|group=lower-alpha}} template or {{notelist}} template (see the help page).
- ^ Wilkins, David (2007). "Section 6: The Extended Real Number System" (PDF). maths.tcd.ie. Retrieved 2019-12-03.
- ^ a b Weisstein, Eric W. "Affinely Extended Real Numbers". mathworld.wolfram.com. Retrieved 2019-12-03.





![{\displaystyle [-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7a5a5ba47896e8fdd43cf7f311db27350f0f8ff)



