Filter (mathematics)

For filters on sets, see Filter (set theory).
For other uses, see Filter (disambiguation).
The power set lattice of the set {1, 2, 3, 4}, with upper set ↑{1, 4} colored dark green. This upper set is a filter, and even a principal filter. It is not an ultrafilter, because including also the light green elements extends it to the larger nontrivial filter ↑{1}. Since the latter cannot be extended further, ↑{1} is an ultrafilter.

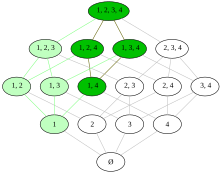
In mathematics, a filter or order filter is a special subset of a partially ordered set (poset), describing "large" or "eventual" elements. Filters appear in order and lattice theory, but also topology, whence they originate. The notion dual to a filter is an order ideal.

Special cases of filters include ultrafilters, which are filters that cannot be enlarged, and describe nonconstructive techniques in mathematical logic.

Filters on sets were introduced by Henri Cartan in 1937. Nicolas Bourbaki, in their book Topologie Générale, popularized filters as an alternative to E. H. Moore and Herman L. Smith's 1922 notion of a net; order filters generalize this notion from the specific case of a power set under inclusion to arbitrary partially ordered sets. Nevertheless, the theory of power-set filters retains interest in its own right, in part for substantial applications in topology.