| Folkman graph | |
|---|---|
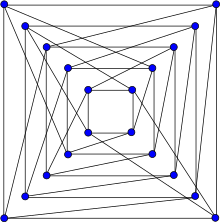 Drawing following Folkman (1967), Figure 1 | |
| Named after | Jon Folkman |
| Vertices | 20 |
| Edges | 40 |
| Radius | 3 |
| Diameter | 4 |
| Girth | 4 |
| Automorphisms | 5! · 25 = 3840 |
| Chromatic number | 2 |
| Chromatic index | 4 |
| Genus | 3 |
| Book thickness | 3 |
| Queue number | 2 |
| Properties | |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the Folkman graph is a 4-regular graph with 20 vertices and 40 edges. It is a regular bipartite graph with symmetries taking every edge to every other edge, but the two sides of its bipartition are not symmetric with each other, making it the smallest possible semi-symmetric graph.[1] It is named after Jon Folkman, who constructed it for this property in 1967.[2]
The Folkman graph can be constructed either using modular arithmetic or as the subdivided double of the five-vertex complete graph. Beyond the investigation of its symmetry, it has also been investigated as a counterexample for certain questions of graph embedding.