Gamma distribution

Gamma

Probability density function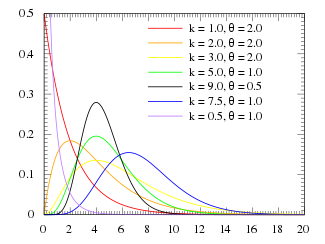
Cumulative distribution function
Parameters	k > 0 shape θ > 0 scale	α > 0 shape β > 0 rate
Support	${\displaystyle x\in (0,\infty )}$	${\displaystyle x\in (0,\infty )}$
PDF	${\displaystyle f(x)={\frac {1}{\Gamma (k)\theta ^{k}}}x^{k-1}e^{-x/\theta }}$	${\displaystyle f(x)={\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}x^{\alpha -1}e^{-\beta x}}$
CDF	${\displaystyle F(x)={\frac {1}{\Gamma (k)}}\gamma \left(k,{\frac {x}{\theta }}\right)}$	${\displaystyle F(x)={\frac {1}{\Gamma (\alpha )}}\gamma (\alpha ,\beta x)}$
Mean	${\displaystyle k\theta }$	${\displaystyle {\frac {\alpha }{\beta }}}$
Median	No simple closed form	No simple closed form
Mode	${\displaystyle (k-1)\theta {\text{ for }}k\geq 1}$, ${\displaystyle 0{\text{ for }}k<1}$	${\displaystyle {\frac {\alpha -1}{\beta }}{\text{ for }}\alpha \geq 1{\text{, }}0{\text{ for }}\alpha <1}$
Variance	${\displaystyle k\theta ^{2}}$	${\displaystyle {\frac {\alpha }{\beta ^{2}}}}$
Skewness	${\displaystyle {\frac {2}{\sqrt {k}}}}$	${\displaystyle {\frac {2}{\sqrt {\alpha }}}}$
Excess kurtosis	${\displaystyle {\frac {6}{k}}}$	${\displaystyle {\frac {6}{\alpha }}}$
Entropy	${\displaystyle {\begin{aligned}k&+\ln \theta +\ln \Gamma (k)\\&+(1-k)\psi (k)\end{aligned}}}$	${\displaystyle {\begin{aligned}\alpha &-\ln \beta +\ln \Gamma (\alpha )\\&+(1-\alpha )\psi (\alpha )\end{aligned}}}$
MGF	${\displaystyle (1-\theta t)^{-k}{\text{ for }}t<{\frac {1}{\theta }}}$	${\displaystyle \left(1-{\frac {t}{\beta }}\right)^{-\alpha }{\text{ for }}t<\beta }$
CF	${\displaystyle (1-\theta it)^{-k}}$	${\displaystyle \left(1-{\frac {it}{\beta }}\right)^{-\alpha }}$
Fisher information	${\displaystyle I(k,\theta )={\begin{pmatrix}\psi ^{(1)}(k)&\theta ^{-1}\\\theta ^{-1}&k\theta ^{-2}\end{pmatrix}}}$	${\displaystyle I(\alpha ,\beta )={\begin{pmatrix}\psi ^{(1)}(\alpha )&-\beta ^{-1}\\-\beta ^{-1}&\alpha \beta ^{-2}\end{pmatrix}}}$
Method of moments	${\displaystyle k={\frac {E[X]^{2}}{V[X]}}\quad \quad }$ ${\displaystyle \theta ={\frac {V[X]}{E[X]}}\quad \quad }$	${\displaystyle \alpha ={\frac {E[X]^{2}}{V[X]}}}$ ${\displaystyle \beta ={\frac {E[X]}{V[X]}}}$

In probability theory and statistics, the gamma distribution is a versatile two-parameter family of continuous probability distributions.^[1] The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution.^[2] There are two equivalent parameterizations in common use:

1. With a shape parameter k and a scale parameter θ
2. With a shape parameter ${\displaystyle \alpha =k}$ and a rate parameter ⁠${\displaystyle \beta =1/\theta }$⁠

In each of these forms, both parameters are positive real numbers.

The distribution has important applications in various fields, including econometrics, Bayesian statistics, life testing.^[3] In econometrics, the (k, θ) parameterization is common for modeling waiting times, such as the time until death, where it often takes the form of an Erlang distribution for integer k values. Bayesian statistics prefer the (α, β) parameterization, utilizing the gamma distribution as a conjugate prior for several inverse scale parameters, facilitating analytical tractability in posterior distribution computations. The probability density and cumulative distribution functions of the gamma distribution vary based on the chosen parameterization, both offering insights into the behavior of gamma-distributed random variables. The gamma distribution is integral to modeling a range of phenomena due to its flexible shape, which can capture various statistical distributions, including the exponential and chi-squared distributions under specific conditions. Its mathematical properties, such as mean, variance, skewness, and higher moments, provide a toolset for statistical analysis and inference. Practical applications of the distribution span several disciplines, underscoring its importance in theoretical and applied statistics.^[4]

The gamma distribution is the maximum entropy probability distribution (both with respect to a uniform base measure and a ${\displaystyle 1/x}$ base measure) for a random variable X for which E[X] = kθ = α/β is fixed and greater than zero, and E[ln X] = ψ(k) + ln θ = ψ(α) − ln β is fixed (ψ is the digamma function).^[5]