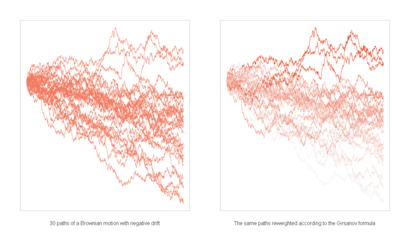
In probability theory, Girsanov's theorem or the Cameron-Martin-Girsanov theorem tells how stochastic processes change under changes in measure. The theorem is especially important in the theory of financial mathematics as it tells how to convert from the physical measure, which describes the probability that an underlying instrument (such as a share price or interest rate) will take a particular value or values, to the risk-neutral measure which is a very useful tool for evaluating the value of derivatives on the underlying.