Gompertz distribution

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (December 2011) (Learn how and when to remove this message)

Gompertz distribution

Probability density function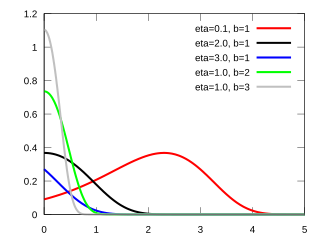
Cumulative distribution function
Parameters	shape ${\displaystyle \eta >0\,\!}$, scale ${\displaystyle b>0\,\!}$
Support	${\displaystyle x\in [0,\infty )\!}$
PDF	${\displaystyle b\eta \exp \left(\eta +bx-\eta e^{bx}\right)}$
CDF	${\displaystyle 1-\exp \left(-\eta \left(e^{bx}-1\right)\right)}$
Quantile	${\displaystyle {\frac {1}{b}}\ln \left(1-{\frac {1}{\eta }}\ln(1-u)\right)}$
Mean	${\displaystyle (1/b)e^{\eta }{\text{Ei}}\left(-\eta \right)}$ ${\displaystyle {\text{where Ei}}\left(z\right)=\int \limits _{-z}^{\infty }\left(e^{-v}/v\right)dv}$
Median	${\displaystyle \left(1/b\right)\ln \left[\left(1/\eta \right)\ln \left(1/2\right)+1\right]}$
Mode	${\displaystyle =\left(1/b\right)\ln \left(1/\eta \right)\ }$ ${\displaystyle {\text{with }}0<{\text{F}}\left(x^{*}\right)<1-e^{-1}=0.632121,0<\eta <1}$ ${\displaystyle =0,\quad \eta \geq 1}$
Variance	${\displaystyle \left(1/b\right)^{2}e^{\eta }\{-2\eta {\ }_{3}{\text{F}}_{3}\left(1,1,1;2,2,2;\eta \right)+\gamma ^{2}}$${\displaystyle +\left(\pi ^{2}/6\right)+2\gamma \ln \left(\eta \right)+[\ln \left(\eta \right)]^{2}-e^{\eta }[{\text{Ei}}\left(-\eta \right)]^{2}\}}$ ${\displaystyle {\begin{aligned}{\text{ where }}&\gamma {\text{ is the Euler constant: }}\,\!\\&\gamma =-\psi \left(1\right)={\text{0.577215... }}\end{aligned}}}$${\displaystyle {\begin{aligned}{\text{ and }}{}_{3}{\text{F}}_{3}&\left(1,1,1;2,2,2;-z\right)=\\&\sum _{k=0}^{\infty }\left[1/\left(k+1\right)^{3}\right]\left(-1\right)^{k}\left(z^{k}/k!\right)\end{aligned}}}$
MGF	${\displaystyle {\text{E}}\left(e^{-tx}\right)=\eta e^{\eta }{\text{E}}_{t/b}\left(\eta \right)}$ ${\displaystyle {\text{with E}}_{t/b}\left(\eta \right)=\int _{1}^{\infty }e^{-\eta v}v^{-t/b}dv,\ t>0}$

In probability and statistics, the Gompertz distribution is a continuous probability distribution, named after Benjamin Gompertz. The Gompertz distribution is often applied to describe the distribution of adult lifespans by demographers^[1][2] and actuaries.^[3][4] Related fields of science such as biology^[5] and gerontology^[6] also considered the Gompertz distribution for the analysis of survival. More recently, computer scientists have also started to model the failure rates of computer code by the Gompertz distribution.^[7] In Marketing Science, it has been used as an individual-level simulation for customer lifetime value modeling.^[8] In network theory, particularly the Erdős–Rényi model, the walk length of a random self-avoiding walk (SAW) is distributed according to the Gompertz distribution.^[9]