| Great dodecicosahedron | |
|---|---|
| |
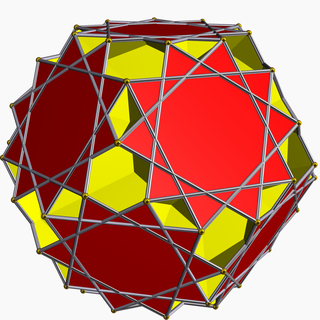
| Type | Uniform star polyhedron |
| Elements | F = 32, E = 120 V = 60 (χ = −28) |
| Faces by sides | 20{6}+12{10/3} |
| Coxeter diagram |     (with extra double-covered triangles) (with extra double-covered pentagons)
|
| Wythoff symbol | 3 5/3 (3/2 5/2) | |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U63, C79, W101 |
| Dual polyhedron | Great dodecicosacron |
| Vertex figure |  6.10/3.6/5.10/7 |
| Bowers acronym | Giddy |
In geometry, the great dodecicosahedron (or great dodekicosahedron) is a nonconvex uniform polyhedron, indexed as U63. It has 32 faces (20 hexagons and 12 decagrams), 120 edges, and 60 vertices.[1] Its vertex figure is a crossed quadrilateral.
It has a composite Wythoff symbol, 3 5⁄3 (3⁄2 5⁄2) |, requiring two different Schwarz triangles to generate it: (3 5⁄3 3⁄2) and (3 5⁄3 5⁄2). (3 5⁄3 3⁄2 | represents the great dodecicosahedron with an extra 12 {10⁄2} pentagons, and 3 5⁄3 5⁄2 | represents it with an extra 20 {6⁄2} triangles.)[2]
Its vertex figure 6.10⁄3.6⁄5.10⁄7 is also ambiguous, having two clockwise and two counterclockwise faces around each vertex.
- ^ Maeder, Roman. "63: great dodecicosahedron". MathConsult.
- ^ Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9. pp. 9–10.