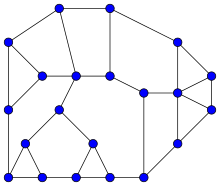
In graph theory, a Halin graph is a type of planar graph, constructed by connecting the leaves of a tree into a cycle. The tree must have at least four vertices, none of which has exactly two neighbors; it should be drawn in the plane so none of its edges cross (this is called a planar embedding), and the cycle connects the leaves in their clockwise ordering in this embedding. Thus, the cycle forms the outer face of the Halin graph, with the tree inside it.[1]
Halin graphs are named after German mathematician Rudolf Halin, who studied them in 1971.[2] The cubic Halin graphs – the ones in which each vertex touches exactly three edges – had already been studied over a century earlier by Kirkman.[3] Halin graphs are polyhedral graphs, meaning that every Halin graph can be used to form the vertices and edges of a convex polyhedron, and the polyhedra formed from them have been called roofless polyhedra or domes.
Every Halin graph has a Hamiltonian cycle through all its vertices, as well as cycles of almost all lengths up to the number of vertices of the graph. Halin graphs can be recognized in linear time. Because Halin graphs have low treewidth, many computational problems that are hard on other kinds of planar graphs, such as finding Hamiltonian cycles, can be solved quickly on Halin graphs.
- ^ Encyclopaedia of Mathematics, first Supplementary volume, 1988, ISBN 0-7923-4709-9, p. 281, article "Halin Graph", and references therein.
- ^ Halin, R. (1971), "Studies on minimally n-connected graphs", Combinatorial Mathematics and its Applications (Proc. Conf., Oxford, 1969), London: Academic Press, pp. 129–136, MR 0278980.
- ^ Cite error: The named reference
kirkmanwas invoked but never defined (see the help page).