| Hemi-dodecahedron | |
|---|---|
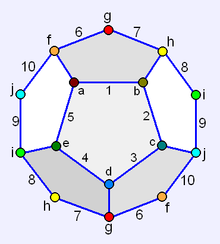 Decagonal Schlegel diagram | |
| Type | Abstract regular polyhedron Globally projective polyhedron |
| Faces | 6 pentagons |
| Edges | 15 |
| Vertices | 10 |
| Euler char. | χ = 1 |
| Vertex configuration | 5.5.5 |
| Schläfli symbol | {5,3}/2 or {5,3}5 |
| Symmetry group | A5, order 60 |
| Dual polyhedron | hemi-icosahedron |
| Properties | Non-orientable |
In geometry, a hemi-dodecahedron is an abstract, regular polyhedron, containing half the faces of a regular dodecahedron. It can be realized as a projective polyhedron (a tessellation of the real projective plane by 6 pentagons), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into three equal parts.
It has 6 pentagonal faces, 15 edges, and 10 vertices.