Holtsmark distribution

Holtsmark
Probability density function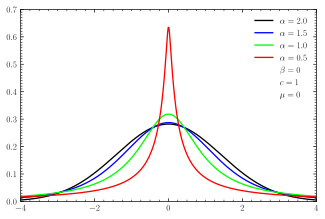
Symmetric stable distributions
Symmetric α-stable distributions with unit scale factor; α=1.5 (blue line) represents the Holtsmark distribution
Cumulative distribution function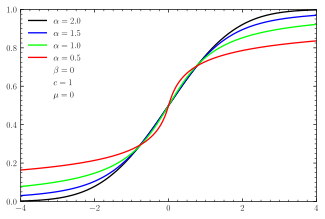
CDF's for symmetric α-stable distributions; α=3/2 represents the Holtsmark distribution
Parameters

c ∈ (0, ∞) — scale parameter

μ ∈ (−∞, ∞) — location parameter
Support x ∈ R
PDF expressible in terms of hypergeometric functions; see text
Mean μ
Median μ
Mode μ
Variance infinite
Skewness undefined
Excess kurtosis undefined
MGF undefined
CF

The (one-dimensional) Holtsmark distribution is a continuous probability distribution. The Holtsmark distribution is a special case of a stable distribution with the index of stability or shape parameter equal to 3/2 and the skewness parameter of zero. Since equals zero, the distribution is symmetric, and thus an example of a symmetric alpha-stable distribution. The Holtsmark distribution is one of the few examples of a stable distribution for which a closed form expression of the probability density function is known. However, its probability density function is not expressible in terms of elementary functions; rather, the probability density function is expressed in terms of hypergeometric functions.

The Holtsmark distribution has applications in plasma physics and astrophysics.[1] In 1919, Norwegian physicist Johan Peter Holtsmark proposed the distribution as a model for the fluctuating fields in plasma due to the motion of charged particles.[2] It is also applicable to other types of Coulomb forces, in particular to modeling of gravitating bodies, and thus is important in astrophysics.[3][4]

  1. ^ Cite error: The named reference lee was invoked but never defined (see the help page).
  2. ^ Holtsmark, J. (1919). "Uber die Verbreiterung von Spektrallinien". Annalen der Physik. 363 (7): 577–630. Bibcode:1919AnP...363..577H. doi:10.1002/andp.19193630702.
  3. ^ Chandrasekhar, S.; J. von Neumann (1942). "The Statistics of the Gravitational Field Arising from a Random Distribution of Stars. I. The Speed of Fluctuations". The Astrophysical Journal. 95: 489. Bibcode:1942ApJ....95..489C. doi:10.1086/144420. ISSN 0004-637X.
  4. ^ Chandrasekhar, S. (1943-01-01). "Stochastic Problems in Physics and Astronomy". Reviews of Modern Physics. 15 (1): 1–89. Bibcode:1943RvMP...15....1C. doi:10.1103/RevModPhys.15.1.