This article needs additional citations for verification. (July 2011) |
| p1m1, (*∞∞) | p2, (22∞) | p2mg, (2*∞) |
|---|---|---|
|

|

|
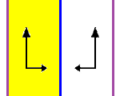
| In 2-dimensions three frieze groups p1m1, p2, and p2mg are isomorphic to the Dih∞ group. They all have 2 generators. The first has two parallel reflection lines, the second two 2-fold gyrations, and the last has one mirror and one 2-fold gyration. | ||

In mathematics, the infinite dihedral group Dih∞ is an infinite group with properties analogous to those of the finite dihedral groups.
In two-dimensional geometry, the infinite dihedral group represents the frieze group symmetry, p1m1, seen as an infinite set of parallel reflections along an axis.