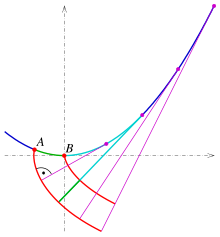
In mathematics, an involute (also known as an evolvent) is a particular type of curve that is dependent on another shape or curve. An involute of a curve is the locus of a point on a piece of taut string as the string is either unwrapped from or wrapped around the curve.[1]
The evolute of an involute is the original curve.
It is generalized by the roulette family of curves. That is, the involutes of a curve are the roulettes of the curve generated by a straight line.
The notions of the involute and evolute of a curve were introduced by Christiaan Huygens in his work titled Horologium oscillatorium sive de motu pendulorum ad horologia aptato demonstrationes geometricae (1673), where he showed that the involute of a cycloid is still a cycloid, thus providing a method for constructing the cycloidal pendulum, which has the useful property that its period is independent of the amplitude of oscillation.[2]
- ^ Rutter, J.W. (2000). Geometry of Curves. CRC Press. pp. 204. ISBN 9781584881667.
- ^ McCleary, John (2013). Geometry from a Differentiable Viewpoint. Cambridge University Press. pp. 89. ISBN 9780521116077.