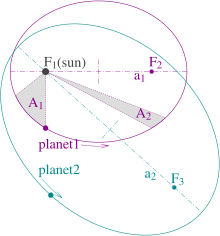
- The orbits are ellipses, with foci F1 and F2 for Planet 1, and F1 and F3 for Planet 2. The Sun is at F1.
- The shaded areas A1 and A2 are equal, and are swept out in equal times by Planet 1's orbit.
- The ratio of Planet 1's orbit time to Planet 2's is .
| Part of a series on |
| Astrodynamics |
|---|
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler in 1609 (except the third law, and was fully published in 1619), describe the orbits of planets around the Sun. These laws replaced circular orbits and epicycles in the heliocentric theory of Nicolaus Copernicus with elliptical orbits and explained how planetary velocities vary. The three laws state that:[1][2]
- The orbit of a planet is an ellipse with the Sun at one of the two foci.
- A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
- The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit.
The elliptical orbits of planets were indicated by calculations of the orbit of Mars. From this, Kepler inferred that other bodies in the Solar System, including those farther away from the Sun, also have elliptical orbits. The second law establishes that when a planet is closer to the Sun, it travels faster. The third law expresses that the farther a planet is from the Sun, the longer its orbital period.
Isaac Newton showed in 1687 that relationships like Kepler's would apply in the Solar System as a consequence of his own laws of motion and law of universal gravitation.
A more precise historical approach is found in Astronomia nova and Epitome Astronomiae Copernicanae.
- ^ "Kepler's Laws". hyperphysics.phy-astr.gsu.edu. Retrieved 2022-12-13.
- ^ "Orbits and Kepler's Laws". NASA Solar System Exploration. Retrieved 2022-12-13.
