| Kite | |
|---|---|
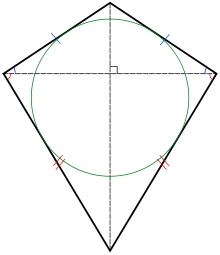 A kite, showing its pairs of equal-length sides and its inscribed circle. | |
| Type | Quadrilateral |
| Edges and vertices | 4 |
| Symmetry group | D1 (*) |
| Dual polygon | Isosceles trapezoid |
In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids,[1] but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals.[2][3] A kite may also be called a dart,[4] particularly if it is not convex.[5][6]
Every kite is an orthodiagonal quadrilateral (its diagonals are at right angles) and, when convex, a tangential quadrilateral (its sides are tangent to an inscribed circle). The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential. They include as special cases the right kites, with two opposite right angles; the rhombi, with two diagonal axes of symmetry; and the squares, which are also special cases of both right kites and rhombi.
The quadrilateral with the greatest ratio of perimeter to diameter is a kite, with 60°, 75°, and 150° angles. Kites of two shapes (one convex and one non-convex) form the prototiles of one of the forms of the Penrose tiling. Kites also form the faces of several face-symmetric polyhedra and tessellations, and have been studied in connection with outer billiards, a problem in the advanced mathematics of dynamical systems.
- ^ Cite error: The named reference
halstedwas invoked but never defined (see the help page). - ^ Cite error: The named reference
goormaghtighwas invoked but never defined (see the help page). - ^ See H. S. M. Coxeter's review of Grünbaum (1960) in MR0125489: "It is unfortunate that the author uses, instead of 'kite', the name 'deltoid', which belongs more properly to a curve, the three-cusped hypocycloid."
- ^ Cite error: The named reference
charter-rogerswas invoked but never defined (see the help page). - ^ Cite error: The named reference
gardnerwas invoked but never defined (see the help page). - ^ Cite error: The named reference
thurstonwas invoked but never defined (see the help page).