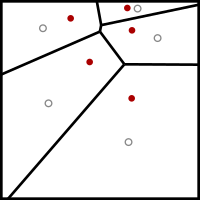
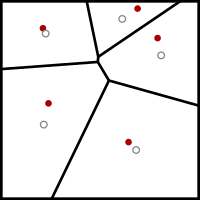
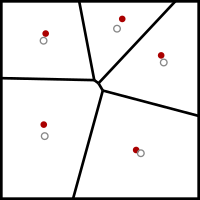
In electrical engineering and computer science, Lloyd's algorithm, also known as Voronoi iteration or relaxation, is an algorithm named after Stuart P. Lloyd for finding evenly spaced sets of points in subsets of Euclidean spaces and partitions of these subsets into well-shaped and uniformly sized convex cells.[1] Like the closely related k-means clustering algorithm, it repeatedly finds the centroid of each set in the partition and then re-partitions the input according to which of these centroids is closest. In this setting, the mean operation is an integral over a region of space, and the nearest centroid operation results in Voronoi diagrams.
Although the algorithm may be applied most directly to the Euclidean plane, similar algorithms may also be applied to higher-dimensional spaces or to spaces with other non-Euclidean metrics. Lloyd's algorithm can be used to construct close approximations to centroidal Voronoi tessellations of the input,[2] which can be used for quantization, dithering, and stippling. Other applications of Lloyd's algorithm include smoothing of triangle meshes in the finite element method.