This article relies largely or entirely on a single source. (June 2013) |
| Logical connectives | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||||||||||||
| Related concepts | ||||||||||||||||||||||
| Applications | ||||||||||||||||||||||
|
| ||||||||||||||||||||||
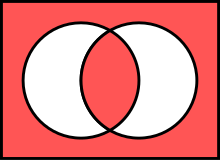
(true part in red)
In logic and mathematics, the logical biconditional, also known as material biconditional or equivalence or biimplication or bientailment, is the logical connective used to conjoin two statements and to form the statement " if and only if " (often abbreviated as " iff "[1]), where is known as the antecedent, and the consequent.[2][3]
Nowadays, notations to represent equivalence include .
is logically equivalent to both and , and the XNOR (exclusive nor) Boolean operator, which means "both or neither".
Semantically, the only case where a logical biconditional is different from a material conditional is the case where the hypothesis (antecedent) is false but the conclusion (consequent) is true. In this case, the result is true for the conditional, but false for the biconditional.[2]
In the conceptual interpretation, P = Q means "All P's are Q's and all Q's are P's". In other words, the sets P and Q coincide: they are identical. However, this does not mean that P and Q need to have the same meaning (e.g., P could be "equiangular trilateral" and Q could be "equilateral triangle"). When phrased as a sentence, the antecedent is the subject and the consequent is the predicate of a universal affirmative proposition (e.g., in the phrase "all men are mortal", "men" is the subject and "mortal" is the predicate).
In the propositional interpretation, means that P implies Q and Q implies P; in other words, the propositions are logically equivalent, in the sense that both are either jointly true or jointly false. Again, this does not mean that they need to have the same meaning, as P could be "the triangle ABC has two equal sides" and Q could be "the triangle ABC has two equal angles". In general, the antecedent is the premise, or the cause, and the consequent is the consequence. When an implication is translated by a hypothetical (or conditional) judgment, the antecedent is called the hypothesis (or the condition) and the consequent is called the thesis.
A common way of demonstrating a biconditional of the form is to demonstrate that and separately (due to its equivalence to the conjunction of the two converse conditionals[2]). Yet another way of demonstrating the same biconditional is by demonstrating that and .
When both members of the biconditional are propositions, it can be separated into two conditionals, of which one is called a theorem and the other its reciprocal.[citation needed] Thus whenever a theorem and its reciprocal are true, we have a biconditional. A simple theorem gives rise to an implication, whose antecedent is the hypothesis and whose consequent is the thesis of the theorem.
It is often said that the hypothesis is the sufficient condition of the thesis, and that the thesis is the necessary condition of the hypothesis. That is, it is sufficient that the hypothesis be true for the thesis to be true, while it is necessary that the thesis be true if the hypothesis were true. When a theorem and its reciprocal are true, its hypothesis is said to be the necessary and sufficient condition of the thesis. That is, the hypothesis is both the cause and the consequence of the thesis at the same time.
- ^ Weisstein, Eric W. "Iff". mathworld.wolfram.com. Retrieved 2019-11-25.
- ^ a b c Peil, Timothy. "Conditionals and Biconditionals". web.mnstate.edu. Archived from the original on 2020-10-24. Retrieved 2019-11-25.
- ^ Brennan, Joseph G. (1961). Handbook of Logic (2nd ed.). Harper & Row. p. 81.










































