A logistic function or logistic curve is a common S-shaped curve (sigmoid curve) with the equation
where
The logistic function has domain the real numbers, the limit as is 0, and the limit as is .
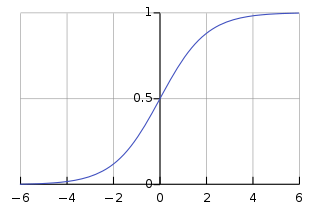
The standard logistic function, depicted at right, where , has the equation
and is sometimes simply called the sigmoid.[2] It is also sometimes called the expit, being the inverse function of the logit.[3][4]
The logistic function finds applications in a range of fields, including biology (especially ecology), biomathematics, chemistry, demography, economics, geoscience, mathematical psychology, probability, sociology, political science, linguistics, statistics, and artificial neural networks. There are various generalizations, depending on the field.
- ^ Verhulst, Pierre-François (1838). "Notice sur la loi que la population poursuit dans son accroissement" (PDF). Correspondance Mathématique et Physique. 10: 113–121. Retrieved 3 December 2014.
- ^ "Sigmoid — PyTorch 1.10.1 documentation".
- ^ expit documentation for R's clusterPower package.
- ^ "Scipy.special.expit — SciPy v1.7.1 Manual".








