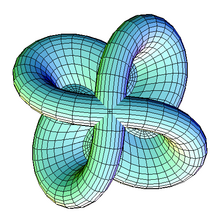



The Morin surface is the half-way model of the sphere eversion discovered by Bernard Morin. It features fourfold rotational symmetry.
If the original sphere to be everted has its outer surface colored green and its inner surface colored red, then when the sphere is transformed through homotopy into a Morin surface, half of the outwardly visible Morin surface will be green, and half red:
Half of a Morin surface corresponds to the exterior (green) of the sphere
to which it is homeomorphic, and the other symmetric half to the interior (red).
Then, rotating the surface 90° around its axis of symmetry will exchange its colors, i.e. will exchange the inner-outer polarity of the orientable surface, so that retracing the steps of the homotopy at exactly the same position back to the original sphere after having so rotated the Morin surface will yield a sphere whose outer surface is red and whose inner surface is green: a sphere which has been turned inside out. The following is a summary of the eversion:
1. sphere: green outside, red inside...
2. transforms into...
3. Morin surface,
3'. Morin surface rotated 90°...
2'. inversely transforms into...
1'. sphere: red outside, green inside.