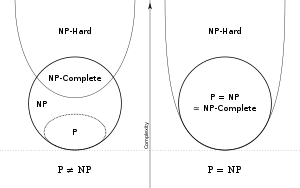
In computational complexity theory, a computational problem H is called NP-hard if, for every problem L which can be solved in non-deterministic polynomial-time, there is a polynomial-time reduction from L to H. That is, assuming a solution for H takes 1 unit time, H's solution can be used to solve L in polynomial time.[1][2] As a consequence, finding a polynomial time algorithm to solve a single NP-hard problem would give polynomial time algorithms for all the problems in the complexity class NP. As it is suspected, but unproven, that P≠NP, it is unlikely that any polynomial-time algorithms for NP-hard problems exist.[3][4]
A simple example of an NP-hard problem is the subset sum problem.
Informally, if H is NP-hard, then it is at least as difficult to solve as the problems in NP. However, the opposite direction is not true: some problems are undecidable, and therefore even more difficult to solve than all problems in NP, but they are probably not NP-hard (unless P=NP).[5]
- ^ Leeuwen, Jan van, ed. (1998). Handbook of Theoretical Computer Science. Vol. A, Algorithms and complexity. Amsterdam: Elsevier. ISBN 0262720140. OCLC 247934368.
- ^ Knuth, Donald (1974). "Postscript about NP-hard problems". ACM SIGACT News. 6 (2): 15–16. doi:10.1145/1008304.1008305. S2CID 46480926.
- ^ Daniel Pierre Bovet; Pierluigi Crescenzi (1994). Introduction to the Theory of Complexity. Prentice Hall. p. 69. ISBN 0-13-915380-2.
- ^ "Shtetl-Optimized » Blog Archive » The Scientific Case for P≠NP". www.scottaaronson.com. Retrieved 2016-09-25.
- ^ "Is undecidable(complement of R) a subset of NP-hard?". Computer Science Stack Exchange. Retrieved 2024-02-09.