NP (complexity)

Unsolved problem in computer science:
(more unsolved problems in computer science)
Euler diagram for P, NP, NP-complete, and NP-hard set of problems. Under the assumption that P ≠ NP, the existence of problems within NP but outside both P and NP-complete was established by Ladner.[1]

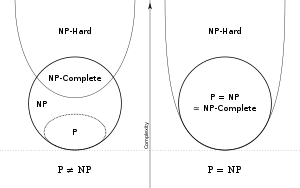
In computational complexity theory, NP (nondeterministic polynomial time) is a complexity class used to classify decision problems. NP is the set of decision problems for which the problem instances, where the answer is "yes", have proofs verifiable in polynomial time by a deterministic Turing machine, or alternatively the set of problems that can be solved in polynomial time by a nondeterministic Turing machine.[2][Note 1]

The first definition is the basis for the abbreviation NP; "nondeterministic, polynomial time". These two definitions are equivalent because the algorithm based on the Turing machine consists of two phases, the first of which consists of a guess about the solution, which is generated in a nondeterministic way, while the second phase consists of a deterministic algorithm that verifies whether the guess is a solution to the problem.[3]

It is easy to see that the complexity class P (all problems solvable, deterministically, in polynomial time) is contained in NP (problems where solutions can be verified in polynomial time), because if a problem is solvable in polynomial time, then a solution is also verifiable in polynomial time by simply solving the problem. It is widely believed, but not proven, that P is smaller than NP, in other words, that decision problems exist that cannot be solved in polynomial time even though their solutions can be checked in polynomial time. The hardest problems in NP are called NP-complete problems. An algorithm solving such a problem in polynomial time is also able to solve any other NP problem in polynomial time. If P were in fact equal to NP, then a polynomial-time algorithm would exist for solving NP-complete, and by corollary, all NP problems.[4]

The complexity class NP is related to the complexity class co-NP, for which the answer "no" can be verified in polynomial time. Whether or not NP = co-NP is another outstanding question in complexity theory.[5]

  1. ^ Ladner, R. E. (1975). "On the structure of polynomial time reducibility". J. ACM. 22: 151–171. doi:10.1145/321864.321877. S2CID 14352974. Corollary 1.1.
  2. ^ Kleinberg, Jon; Tardos, Éva (2006). Algorithm Design (2nd ed.). Addison-Wesley. p. 464. ISBN 0-321-37291-3.
  3. ^ Alsuwaiyel, M. H.: Algorithms: Design Techniques and Analysis, p. 283.
  4. ^ William Gasarch (June 2002). "The P=?NP poll" (PDF). SIGACT News. 33 (2): 34–47. doi:10.1145/1052796.1052804. S2CID 18759797. Retrieved 2008-12-29.
  5. ^ Kleinberg, Jon; Tardos, Éva (2006). Algorithm Design (2nd ed.). p. 496. ISBN 0-321-37291-3.


Cite error: There are <ref group=Note> tags on this page, but the references will not show without a {{reflist|group=Note}} template (see the help page).