| Nonconvex great rhombicuboctahedron | |
|---|---|
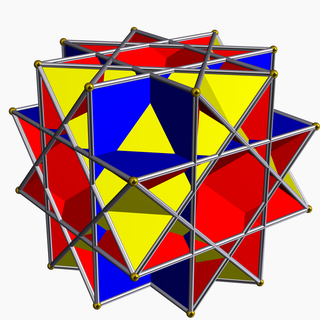
| |
| Type | Uniform star polyhedron |
| Elements | F = 26, E = 48 V = 24 (χ = 2) |
| Faces by sides | 8{3}+(6+12){4} |
| Coxeter diagram | |
| Wythoff symbol | 3/2 4 | 2 3 4/3 | 2 |
| Symmetry group | Oh, [4,3], *432 |
| Index references | U17, C59, W85 |
| Dual polyhedron | Great deltoidal icositetrahedron |
| Vertex figure |  4.4.4.3/2 |
| Bowers acronym | Querco |

In geometry, the nonconvex great rhombicuboctahedron is a nonconvex uniform polyhedron, indexed as U17. It has 26 faces (8 triangles and 18 squares), 48 edges, and 24 vertices.[1] It is represented by the Schläfli symbol rr{4,3⁄2} and Coxeter-Dynkin diagram of ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Its vertex figure is a crossed quadrilateral.
. Its vertex figure is a crossed quadrilateral.
This model shares the name with the convex great rhombicuboctahedron, also called the truncated cuboctahedron.
An alternative name for this figure is quasirhombicuboctahedron. From that derives its Bowers acronym: querco.
- ^ Maeder, Roman. "17: great rhombicuboctahedron". MathConsult.