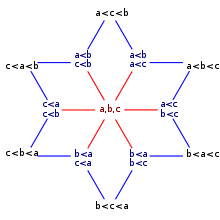
In number theory and enumerative combinatorics, the ordered Bell numbers or Fubini numbers count the weak orderings on a set of elements. Weak orderings arrange their elements into a sequence allowing ties, such as might arise as the outcome of a horse race.[1][2]
The ordered Bell numbers were studied in the 19th century by Arthur Cayley and William Allen Whitworth. They are named after Eric Temple Bell, who wrote about the Bell numbers, which count the partitions of a set; the ordered Bell numbers count partitions that have been equipped with a total order. Their alternative name, the Fubini numbers, comes from a connection to Guido Fubini and Fubini's theorem on equivalent forms of multiple integrals. Because weak orderings have many names, ordered Bell numbers may also be called by those names, for instance as the numbers of preferential arrangements[3] or the numbers of asymmetric generalized weak orders.[4]
These numbers may be computed via a summation formula involving binomial coefficients, or by using a recurrence relation. They also count combinatorial objects that have a bijective correspondence to the weak orderings, such as the ordered multiplicative partitions of a squarefree number[5] or the faces of all dimensions of a permutohedron.[6]
- ^ Cite error: The named reference
horsewas invoked but never defined (see the help page). - ^ Cite error: The named reference
mendelsonwas invoked but never defined (see the help page). - ^ Cite error: The named reference
grosswas invoked but never defined (see the help page). - ^ Cite error: The named reference
oeiswas invoked but never defined (see the help page). - ^ Cite error: The named reference
sklarwas invoked but never defined (see the help page). - ^ Cite error: The named reference
zieglerwas invoked but never defined (see the help page).
