This article needs additional citations for verification. (March 2021) |
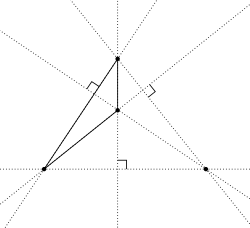
In geometry, an orthocentric system is a set of four points on a plane, one of which is the orthocenter of the triangle formed by the other three. Equivalently, the lines passing through disjoint pairs among the points are perpendicular, and the four circles passing through any three of the four points have the same radius.[1]
If four points form an orthocentric system, then each of the four points is the orthocenter of the other three. These four possible triangles will all have the same nine-point circle. Consequently these four possible triangles must all have circumcircles with the same circumradius.
- ^ Kocik, Jerzy; Solecki, Andrzej (2009). "Disentangling a triangle" (PDF). American Mathematical Monthly. 116 (3): 228–237. doi:10.1080/00029890.2009.11920932.